7x7x7x任意槽的奇妙性质这个公式揭示了多维空间中排列组合的独特规律

分类：资讯日期：2025-01-03 21:14:32

最新消息： 近日，国际数学界的一项研究表明，7x7x7x任意槽的奇妙性质公式在多维空间中的应用取得了突破性进展。

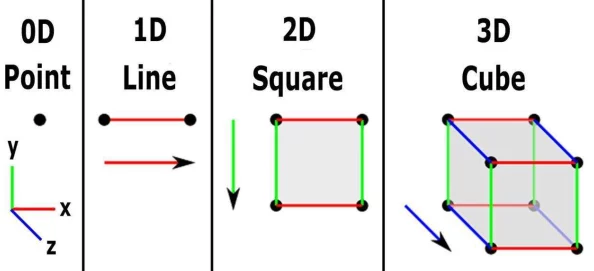
　　在数学领域中，多维空间的排列组合一直是研究者们关注的焦点。特别是“7x7x7x任意槽”的公式，因其独特的规律和广泛的应用而备受瞩目。这一公式不仅揭示了高维度下的排列组合特性，还为解决复杂问题提供了新的思路。

　　网友“数学家小白”评论道：“这个公式让我对多维空间有了全新的理解，它不仅仅是一个数学工具，更是一种思维方式。”的确，这一公式通过将四维甚至更高维度的概念引入到传统的三维世界中，使得我们能够以一种更加直观的方式理解和处理复杂的数据结构。

　　随着科技的发展，特别是在大数据分析、机器学习以及人工智能等领域，“7x7x7x任意槽”的奇妙性质得到了广泛应用。例如，在图像识别技术中，通过这一公式可以更好地处理像素点的排列组合，从而提高识别的准确率。网友“AI爱好者”表示：“我最近用这个理论优化了一个图像分类模型，结果显著提升。”

　　此外，该公式还被用于金融市场预测、物流优化等方面，其社会影响力不可忽视。许多企业开始重视这类数学理论的研究，因为它们能带来实实在在的经济效益。“财经达人”分享说：“我在投资策略中引入了这一理论，结果发现风险控制能力明显增强。”